Ngày đăng: 22/07/2020
Cộng đồng zalo giải đáo bài tập
Các bạn học sinh tham gia nhóm zalo để trao đổi giải đáp bài tập nhé
| Con sinh năm 2009 | https://zalo.me/g/cieyke829 |
| Con sinh năm 2010 | https://zalo.me/g/seyfiw173 |
| Con sinh năm 2011 | https://zalo.me/g/jldjoj592 |
| Con sinh năm 2012 | https://zalo.me/g/ormbwj717 |
| Con sinh năm 2013 | https://zalo.me/g/lxfwgf190 |
| Con sinh năm 2014 | https://zalo.me/g/bmlfsd967 |
| Con sinh năm 2015 | https://zalo.me/g/klszcb046 |
$$ $$ BÀI 3 – ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT
I.Lý thuyết:
1. Đồ thị của hàm số $y=ax;\left( a\ne 0 \right)$
Đồ thị của hàm số $y=ax;\left( a\ne 0 \right)$ là một đường thẳng đi qua gốc tọa độ và điểm $A\left( 1;a \right)$. Như vậy, để vẽ đồ thị hàm số $y=ax;\left( a\ne 0 \right)$, ta thực hiện:
+ Xác định vị trí điểm $A\left( 1;a \right)$
+ Nối O với A ta được đồ thị hàm số $y=ax$
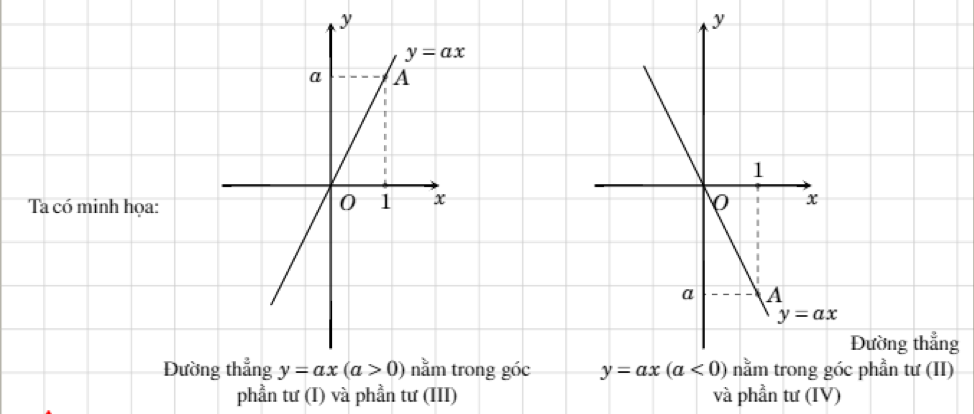
Chú ý: Ta có một số chú ý sau:
+ Đồ thị hàm số $y=x$ chính là đường phân giác của góc phần tư thứ I, III
+ Đồ thị hàm số $y=-x$ chính là đường phân giác của góc phần tư thứ II, IV.
2.Đồ thị của hàm số $y=ax+b;\left( a\ne 0 \right)$
Đồ thị hàm số $y=ax+b,\left( a\ne 0 \right)$ là một đường thẳng cắt trục tung tại điểm có tung độ bằng b. Đường thẳng này:
+ Song song với đường thẳng $y=ax$ nếu $b\ne 0$
+ Trùng với đường thẳng $y=ax$ nếu $b=0$
Từ kết quả trên ta thấy: Nếu đã có đồ thị hàm số $y=ax$ thì đồ thị hàm số $y=ax+b;b\ne 0$ được suy ra bằng cách:
+ Xác định vị trí điểm $M\left( 0;b \right)$
+ Đường thẳng đi qua M song song với đường thẳng $y=ax$ chính là đồ thị hàm số $y=ax+b$
3. Cách vẽ đồ thị hàm số bậc nhất
Vì đồ thị hàm số bậc nhất là một đường thẳng nên muốn vẽ ta chỉ cần xác định hai điểm phân biệt bất kỳ trên đường thẳng đó.
Chú ý:
Khi vẽ đồ thị hàm số $y=ax+b;a\ne 0$ ta nên chọn hai điểm có tọa độ chẵn
Thông thường ta chọn hai điểm $A\left( 0;b \right)$ và $B\left( -\frac{b}{a};0 \right)$ theo thứ tự giao điểm của đồ thị với trục Oy và Ox nếu hai điểm đó không nằm quá xa gốc tọa độ (ví dụ $y=x+2005$ ) hoặc tọa độ của chúng không quá phức tạp trong tính toán
II .Các dạng toán
1.Dạng 1. Vẽ đồ thị hàm số. Tìm giao điểm của hai đồ thị
Phương pháp giải:
Để vẽ đồ thị hàm số, ta tìm hai điểm mà đồ thị hàm số đi qua rồi nối chúng lại (thường tìm giao với hai trục tọa độ)
- Để tìm giao điểm đồ thị hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$. Ta xét phương trình hoành độ giao điểm:$f\left( x \right)=g\left( x \right)$ tìm được ${{x}_{0}}$ rồi tính ${{y}_{0}}=f\left( {{x}_{0}} \right)$ suy ra giao điểm $A\left( {{x}_{0}};{{y}_{0}} \right)$
Ví dụ 1.
Cho hàm số $y=-x+3$
a) Xác định giao điểm của đồ thị hàm số với trục tung và trục hoành. Vẽ đồ thị hàm số
b) Gọi A và B theo thứ tự là hai giao điểm nói trên. Tính diện tích tam giác OAB (O là gốc tọa độ)
c) Gọi $\alpha $ là góc nhọn tạo bởi đồ thị hàm số với trục $Ox$. Tìm $\tan \alpha $, suy ra số đo góc $\alpha $
d) Bằng đồ thị, tìm $x$ để $y>0;y\le 0$
Bài giải:
a)
Đồ thị cắt trục Oy tại A có:
$x=0\Rightarrow y=-0+3=3\Rightarrow A\left( 0;3 \right)$
Đồ thị cắt trục Ox tại B có:
$y=0\Rightarrow 0=-x+3\Rightarrow x=3\Rightarrow B\left( 3;0 \right)$
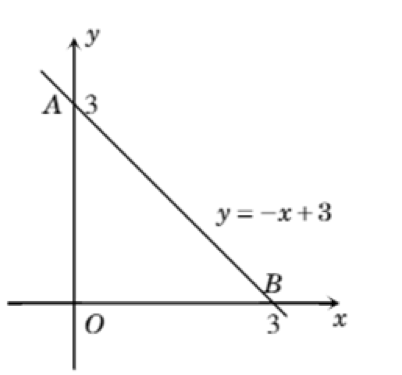
b)
Ta có:
${{S}_{\Delta OAB}}=\frac{1}{2}OA.OB=\frac{1}{2}.3.3=\frac{9}{2}$
c)
Xét:
$\Delta OAB;\widehat{OBA}=\alpha $
$\Rightarrow \tan \alpha =\frac{OA}{OB}=\frac{3}{3}=1\Rightarrow \alpha ={{45}^{0}}$
d)
Từ đồ thị suy ra:
$y>0\Leftrightarrow x3$, ứng với phần đồ thị nằm phía trên trục $Ox$
$y\le 0\Leftrightarrow x\ge 3$, ứng với phần đồ thị phía dưới trục Ox
Ví dụ 2.
Cho hàm số $y=ax-3a$
a) Xác định giá trị của $a$ để đồ thị hàm số đi qua điểm $A\left( 0;4 \right)$. Vẽ đồ thị hàm số với $a$ vừa tìm được.
b) Tính khoảng cách từ gốc tọa độ đến đường thẳng tìm được trong $a)$
Bài giải:
a) Đồ thị hàm số đi qua điểm $A\left( 0;4 \right)$ khi và chỉ khi : $4=a.0-3a\Leftrightarrow 3a=-4\Leftrightarrow a=-\frac{4}{3}$
Vậy hàm số có dạng $y=-\frac{4}{3}x+4$
Để vẽ đồ thị hàm số ta lấy thêm điểm $B\left( 3;0 \right)$
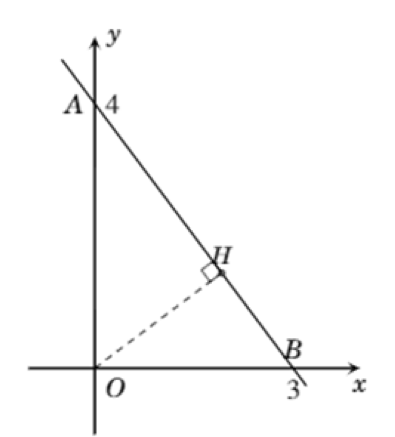
b) Gọi H là hình chiếu vuông góc của O lên đường thẳng AB.
Trong $\Delta OAB$ vuông tại O, ta có:
$\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}$
$\Leftrightarrow OH=\frac{OA.OB}{\sqrt{O{{A}^{2}}+O{{B}^{2}}}}=\frac{4.3}{\sqrt{{{4}^{3}}+{{3}^{2}}}}=\frac{12}{5}$
Ví dụ 3.
Cho hai hàm số $y=2x;y=-\frac{1}{2}x$
a) Vẽ trên cùng một hệ trục tọa độ $Oxy$ đồ thị của các hàm số. Có nhận xét gì về đồ thị của hàm số này?
b) Xác định tọa độ điểm B thuộc đồ thị hàm số $y=-\frac{1}{2}x$ sao cho ${{x}_{B}}=4{{y}_{B}}+2$
Bài giải:
a)
Để vẽ đồ thị hàm số $y=2x$ ta thực hiện:
+ Xác định thêm một điểm $A\left( 1;2 \right)$
+ Nối O với A ta được đồ thị $y=2x$
Để vẽ đồ thị hàm số $y=-\frac{1}{2}x$ ta thực hiện:
+ Xác định thêm một điểm $B\left( -2;1 \right)$
+ Nối O với B ta được đồ thị $y=-\frac{1}{2}x$
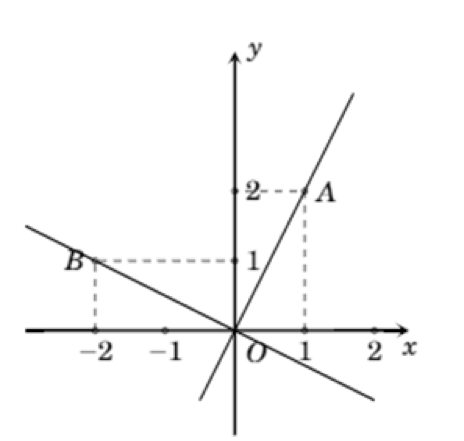
Nhận xét: Đồ thị hai hàm số này vuông góc với nhau
b)
B thuộc đồ thị hàm số $y=-\frac{1}{2}x$ suy ra ${{y}_{B}}=-\frac{1}{2}{{x}_{B}}\left( * \right)$
Thay ${{x}_{B}}=4{{y}_{B}}+2$ vào (*) ta được:
${{y}_{B}}=-\frac{1}{2}\left( 4{{y}_{B}}+2 \right)\Rightarrow {{y}_{B}}=-\frac{1}{3}$
$\Rightarrow {{x}_{B}}=4\left( -\frac{1}{3} \right)+2=\frac{2}{3}$
Vậy điểm $B\left( -\frac{1}{3};\frac{2}{3} \right)$ là điểm cần tìm
2.Dạng 2. Vẽ đồ thị hàm số chứa dấu giá trị tuyệt đối
Phương pháp giải:
a) Vẽ đồ thị hàm số $y=\left| f\left( x \right) \right|$
Cách 1: Dùng quy tắc phá dấu giá trị tuyệt đối rồi vẽ
Cách 2:
+ Vẽ đồ thị hàm số $y=f\left( x \right)$
+ Giữ nguyên phần đồ thị phía trên trục Ox của $y=f\left( x \right)$ (P1)
+ Lấy đối xứng phần đồ thị phía dưới trục Ox của $y=f\left( x \right)$ lên phía trên Ox ta được (P2)
+ Đồ thị $y=\left| f\left( x \right) \right|$ là P1 và P2
b) Vẽ đồ thị hàm số $y=f\left( \left| x \right| \right)$
+ Vẽ đồ thị hàm số $y=f\left( x \right)$
+ Lấy đối xứng qua Oy phần đồ thị bên phải Oy của $y=f\left( x \right)$
+ Đồ thị $y=f\left( \left| x \right| \right)$ là phần bên phải và phần lấy đối xứng
Ví dụ 4.
Vẽ đồ thị các hàm số sau:
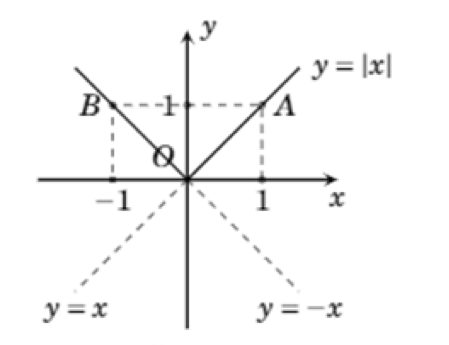
a) $y=\left| x \right|$
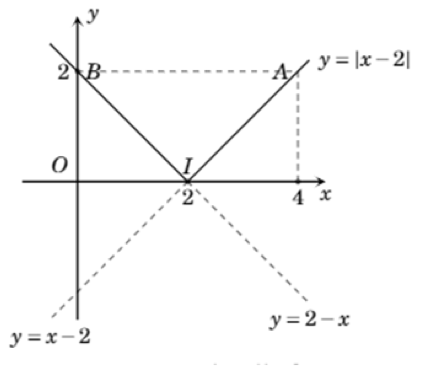
b) $y=\left| x-2 \right|$
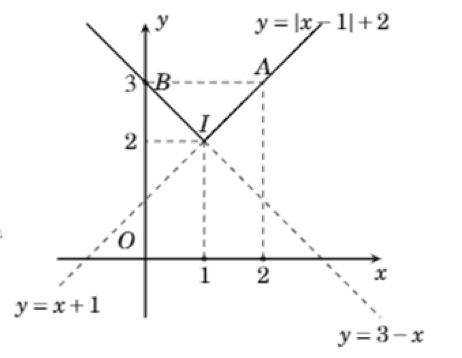
c) $y=\left| x-1 \right|+2$
Bài giải:
a)
Ta có:
$y=\left| x \right|=$ $\left\{ \begin{align}& x\,\,neu\,x\ge 0 \\ & -x\,\,neu\,x0 \\ \end{align} \right.$
Do đó đồ thị hàm số là hai tia OA với $A\left( 1;1 \right)$ và OB với $B\left( -1;1 \right)$
b)
Ta có:
$y=\left| x-2 \right|=$$\left\{ \begin{align}& x-2\,\,neu\,x\ge 2 \\ & 2-x\,\,neu\,x2 \\ \end{align} \right.$
Do đó đồ thị hàm số là hai tia IA với $I\left( 2;0 \right)$ và IB với $B\left( 0;2 \right)$
c)
Ta có:
$y=\left| x-1 \right|+2$ $=\left\{ \begin{align}& x+1\,\,neu\,x\ge 1 \\ & 3-x\,\,neu\,x1 \\\end{align} \right.$
Do đó đồ thị hàm số là hai tia IA với $A\left( 1;2 \right)$ và IB với $B\left( 0;3 \right)$
III. Bài tập tự luyện
Bài 1.
Vẽ đồ thị các hàm số:
a) $y=4x$
b) $y=x+3$
c) $y=-x+6$
d) $y=-3x-3$
e) $y=-\frac{1}{2}x+1$
Bài 2.
Cho hàm số $y=ax$. Hãy xác định hệ số $a$ biết:
a) Đồ thị hàm số đi qua điểm A(1;8)
b) Đồ thị hàm số đi qua điểm $B\left( \frac{3}{4};-3 \right)$
c) Đồ thị hàm số là đường phân giác của góc phần từ thứ I, III
Vẽ đồ thị hàm số trong mỗi trường hợp trên.
Bài 3.
Cho hàm số $y=\left( 2a-3 \right)x$ . Hãy xác định $a$ để:
a) Hàm số luôn đồng biến? Nghịch biến
b) Đồ thị hàm số đi qua điểm A(2;3)
c) Đồ thị hàm số đi qua điểm $B\left( \frac{5}{4};-\frac{1}{2} \right)$
d) Đồ thị hàm số là đường phân giác góc phần tư thứ II, IV
Vẽ đồ thị hàm số trong mỗi trường hợp b), c), d)
Bài 4.
Cho hàm số $y=2ax-3a$
a) Xác định $a$ biết đồ thị hàm số trên đi qua điểm M(2;3)
b) Vẽ đồ thị hàm số tìm được trong a)
c) Tính khoảng cách từ gốc tọa độ đến đường thẳng tìm được trong a)
Bài 5.
Cho hàm số $y=ax+b$
a) Xác định a và b biết rằng đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -4 và cắt trục hoành tại điểm có hoành độ bằng 1
b) Vẽ đồ thị hàm số tìm được trong a)
c) Tính diện tích tam giác được tạo bởi đồ thị hàm số trong a) và các trục tọa độ
Bài 6.
Vẽ đồ thị các hàm số sau:
a) $y=\left| x \right|$
b) $y=2\left| x \right|-1$
c) $y=\left| -\frac{x}{2}+2 \right|$
d) $y=\left| \frac{3}{4}x+\frac{1}{4} \right|$
e) $y=\left| -\frac{x}{2}+2 \right|$
$$
Tác giả: Vinastudy
Cộng đồng zalo giải đáo bài tập
Các bạn học sinh tham gia nhóm zalo để trao đổi giải đáp bài tập nhé
| Con sinh năm 2009 | https://zalo.me/g/cieyke829 |
| Con sinh năm 2010 | https://zalo.me/g/seyfiw173 |
| Con sinh năm 2011 | https://zalo.me/g/jldjoj592 |
| Con sinh năm 2012 | https://zalo.me/g/ormbwj717 |
| Con sinh năm 2013 | https://zalo.me/g/lxfwgf190 |
| Con sinh năm 2014 | https://zalo.me/g/bmlfsd967 |
| Con sinh năm 2015 | https://zalo.me/g/klszcb046 |
********************************
Hỗ trợ học tập:
_Kênh Youtube:http://bit.ly/vinastudyvn_tieuhoc
_Facebook fanpage:https://www.facebook.com/767562413360963/
_Hội học sinh Vinastudy Online:https://www.facebook.com/groups/online.duhocuc24h.edu.vn/