Vẽ tia phân giác của một góc đơn giản với 5 cách sau đây

Vẽ hình là 1 mạch kỹ năng và kiến thức khá thú vị nhập Toán học tập, nó và được những ngôi nhà Toán học tập nghiên cứu và phân tích từ không ít thế kỉ trước công nguyên vẹn.

Hầu không còn những mối liên hệ, những hình cơ phiên bản đều rất có thể vẽ được, tiêu biểu vượt trội là vẽ một quãng trực tiếp bởi vì một quãng trực tiếp mang đến trước, vẽ một góc bởi vì một góc mang đến trước, vẽ lối trung trực của một quãng trực tiếp, vẽ tam giác, …

Bạn đang xem: Vẽ tia phân giác của một góc đơn giản với 5 cách sau đây

Và thời điểm ngày hôm nay tất cả chúng ta tiếp tục cùng với nhau dò thám hiểu về cách vẽ tia phân giác của một góc, đó cũng là 1 trong mỗi đối tượng người tiêu dùng thông thường bắt gặp nhất khi chúng ta thực hiện những bài xích tập luyện hình học tập.

I. Như thế này thì được gọi là tia phân giác của một góc?

Định nghĩa: Tia phân giác của một góc là tia nằm trong lòng nhị cạnh của góc và tạo ra với nhị cạnh ấy nhị góc bởi vì nhau:

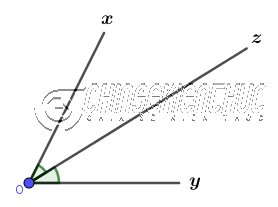
• Tia Oz nằm trong lòng nhị tia Ox, Oy
• Tia Oz phân tách $\widehat{xOy}$ trở thành $\widehat{xOz}$ và $\widehat{yOz}$
• $\widehat{xOz}=\widehat{yOz}$

=> Vậy tia Oz là tia phân giác của $\widehat{xOy}$

Định nghĩa bên trên rất có thể tuyên bố bên dưới dạng kí hiệu Toán học tập thuần tùy là $\left\{\begin{array}{} \widehat{xOz}+\widehat{zOy}=\widehat{xOy} \\ \widehat{xOz}=\widehat{zOy} \end{array}\right.$ hoặc $\widehat{xOz}=\widehat{zOy}=\frac{\widehat{xOy}}{2}$

Chú ý:

• Đường trực tiếp chứa chấp tia phân giác được gọi là lối phân giác
• Mỗi một góc chỉ mất độc nhất một tia phân giác, nước ngoài trừ góc bẹt.

II. Cách vẽ tia phân giác của một góc

Dưới đấy là năm cách vẽ tia phân giác của một góc thông thường bắt gặp nhất. Tùy theo dõi vấn đề ví dụ thế nào nhưng mà tất cả chúng ta tiếp tục quan tâm đến, lựa lựa chọn cách thức mang đến tương thích nhất.

Cách #1. Sử dụng thước đo góc

Giả sử tất cả chúng ta cần thiết vẽ tia phân giác Oz của $\widehat{xOy}=120^o$

Vì tia Oz là tia phân giác của $\widehat{xOy}$ nên tớ đem $\left\{\begin{array}{} \widehat{xOz}+\widehat{zOy}=120^o \\ \widehat{xOz}=\widehat{zOy}  \end{array}\right.$

=> $\widehat{xOz}=\frac{120}{2}=60^o$

Vậy tớ chỉ việc vẽ tia Oz nằm trong lòng nhị tia Ox và Oy sao mang đến $\widehat{xOz}=60^o$

Bước 1. Vẽ $\widehat{xOy}=120^o$

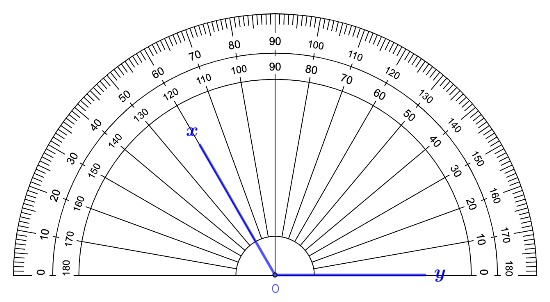
Bước 2. Vẽ $\widehat{xOz}=60^o$

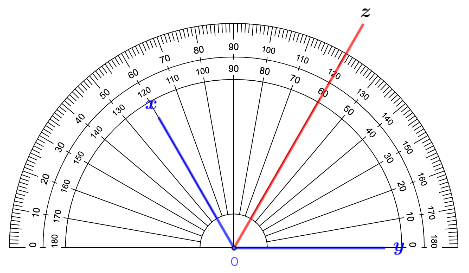
Bước 3. Vẽ kí hiệu $\widehat{xOz}=\widehat{zOx}$

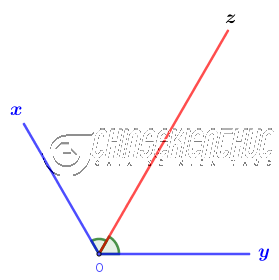
Cách #2. Gấp giấy

Giả sử tất cả chúng ta cần thiết vẽ tia phân giác $Oz$ của $\widehat{xOy}=64^o$

Bước 1. Vẽ $\widehat{xOy}$ lên giấy tờ.

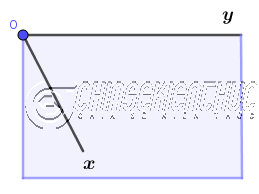
Bước 2. Tiến hành vội vã giấy tờ sao mang đến cạnh Ox trùng với cạnh Oy, khi cơ nếp vội vã tiếp tục mang đến tất cả chúng ta biết đúng mực địa điểm của tia phân giác.

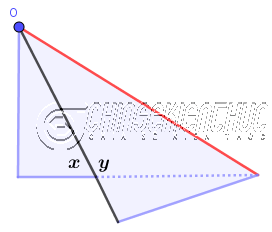
Bước 3. Vẽ tia phân giác theo dõi nếp vội vã vừa phải vội vã được.

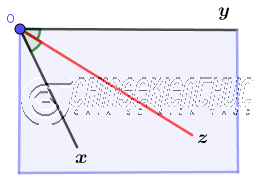
Cách #3. Sử dụng thước trực tiếp (có phân tách vạch)

Giả sử tất cả chúng ta cần thiết vẽ tia phân giác $Oz$ của $\widehat{xOy}$

Bước 1. Trên tia Ox dựng nhị điểm A, B bất kì.

Xem thêm:  Vùng phía Đông Hoa Kì gồm: | cungthi.online

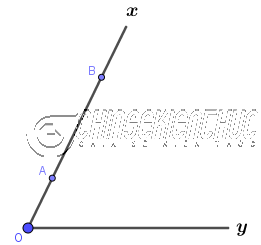
Bước 2. Trên tia Oy dựng nhị điểm C, D sao mang đến OA = OC, OB = OD.

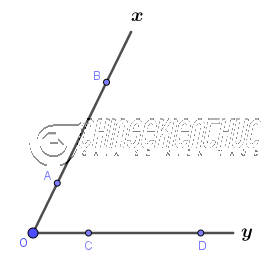
Bước 3. Dựng đoạn trực tiếp AD, CB.

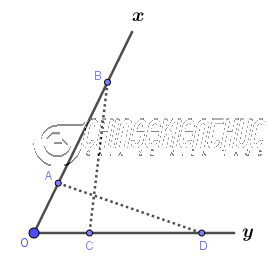
Bước 4. Dựng giao phó điểm E của đoạn trực tiếp AD và CB.

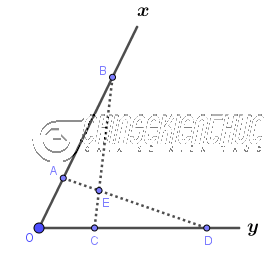
Bước 5. Dựng tia OE => và tia OE đó là tia phân giác của $\widehat{xOy}$

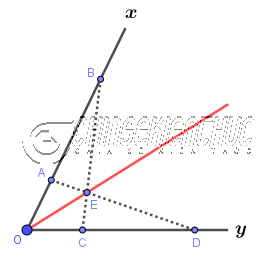
Cách #4. Sử dụng Compa

Chi tiết quá trình tiến hành chúng ta sướng lòng coi phần #1 nhập mục II của nội dung bài viết này nhé !

Cách #5. Sử dụng thước trực tiếp (không đem phân tách vạch)

Giả sử tất cả chúng ta cần thiết vẽ tia phân giác $Oz$ của $\widehat{xOy}$

Bước 1. Đặt thước trực tiếp sao cho 1 lề trùng với tia Ox, vẽ một đường thẳng liền mạch trùng với lề còn sót lại.

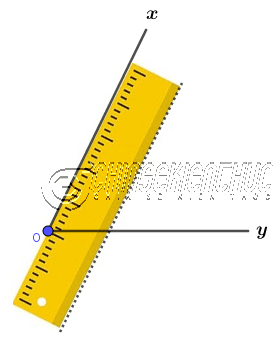
Bước 2. Đặt thước trực tiếp sao cho 1 lề trùng với tia Oy, vẽ một đường thẳng liền mạch trùng với lề còn lại

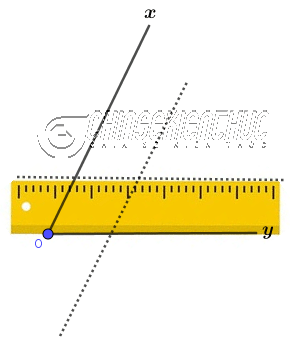
Bước 3. Dựng giao phó điểm của hai tuyến phố trực tiếp ở Bước 1 và Bước 2

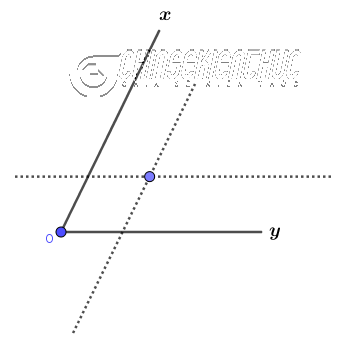
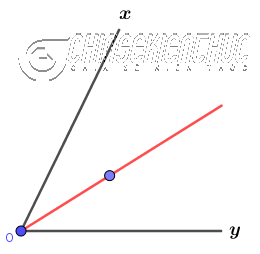
Bước 4. Vẽ tia khởi nguồn từ điểm O qua chuyện giao phó điểm vừa phải dựng => Như vậy tia nhưng mà tất cả chúng ta vừa phải vẽ đó là tia phân giác của $\widehat{xOy}$.

III. Lời kết

Vâng, bên trên đấy là 5 cách vẽ tia phân giác của một góc giản dị nhất nhưng mà chúng ta cũng có thể vận dụng.

Để vẽ hình thì cần phải có dụng cụ vẽ hình, đem thật nhiều dụng cụ vẽ hình không giống nhau như thước trực tiếp (không phân tách vạch hoặc đem phân tách vạch), Compa, Eke, thước đo góc, …

Nếu chỉ dùng độc nhất nhị dụng cụ là thước trực tiếp (không phân tách vạch) và Compa thì người tớ tiếp tục gọi là Dựng hình

Để đảm nói rằng những thao tác vừa phải dựng chính đắn, tất cả chúng ta rất cần phải tiến hành tăng quá trình minh chứng.

Tuy nhiên nhập phạm vi cộc gọn gàng của nội dung bài viết này bản thân tạm thời bỏ dở công đoạn này, nếu còn muốn chúng ta cũng có thể dò thám cơ hội minh chứng test nhé.

Hi vọng là nội dung bài viết này tiếp tục hữu ích với chúng ta. Xin Chào thân ái và hứa hội ngộ chúng ta trong mỗi nội dung bài viết tiếp theo sau !

Đọc thêm:

Xem thêm: Phát biểu nào sau đây về thư điện tử là sai? A. Hai người có thể có địa chỉ thư giống nhau...

• Làm thế này nhằm vẽ lối tròn trặn nội tiếp tam giác?
• 11 loại góc thông thường bắt gặp nhập hình học tập chắc chắn cần biết
• 3 phương pháp vẽ trung điểm của đoạn trực tiếp nhưng mà bản thân hoặc áp dụng

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com